| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 8puzzle
- NeuralNetwork
- MDSR
- SRCNN
- PYTHON
- deeplearning
- pixelshuffle
- AStar
- 동적계획법
- EDSR
- convolution
- CNN
- DFS
- residuallearning
- 딥러닝
- 신경망
- 지도학습
- Increasing Triplet Subsequence
- 비지도학습
- sr
- 준지도학습
- BFS
- leetcode
- residualnetwork
- RESNET
- a*
- 증가하는부분수열
- superresolution
- 합성곱
- Today
- Total
이것저것 코딩하는 블로그
[Algorithm] 8-puzzle: DFS, BFS, A* 본문
0. 8-puzzle 문제
백준의 문제 정의를 참고하겠다. 다만 나는 최단 경로의 길이를 찾는 것이 아닌 모든 노드를 방문하여 탐색하는 방식으로 구현했다.
1525번: 퍼즐
세 줄에 걸쳐서 표에 채워져 있는 아홉 개의 수가 주어진다. 한 줄에 세 개의 수가 주어지며, 빈 칸은 0으로 나타낸다.
www.acmicpc.net
다만 여기서는 정답 노드를 시계 방향 [1 2 3], [8, 0, 4], [7, 6, 5] 로 하였다.
1. DFS (Depth-First Search) - Stack을 이용하여
DFS는 맹목적 탐색의 한 방법으로, 초기 노드에서 깊이 방향으로 탐색하고, 목표 노드에 도달하면 종료하고, 더 이상 진행할 수 없으면 부모 노드로 돌아가는 (backtracking) 방식을 사용한다. 그리고 방문한 노드는 재방문하지 않는다.
한 노드를 선택하면 그 노드의 자식 중 하나를 탐색하고, 탐색한 노드의 자식 중 하나를 계속하여 탐색하는 방식이다.이는 stack을 이용하여 구현할 수 있다. stack은 나중에 들어온 인자를 가장 먼저 반환하기 때문이다. 한 노드의 자식을 생성했으면 그 노드의 자식들이 모두 stack에 순서대로 담기고, 자식 노드 중 하나가 pop 되고 그 자식들을 모두 다시 stack에 담는 과정을 반복하기 때문에 DFS를 구현하기에 적합하다. 자세한 설명은 그림으로 대체한다.
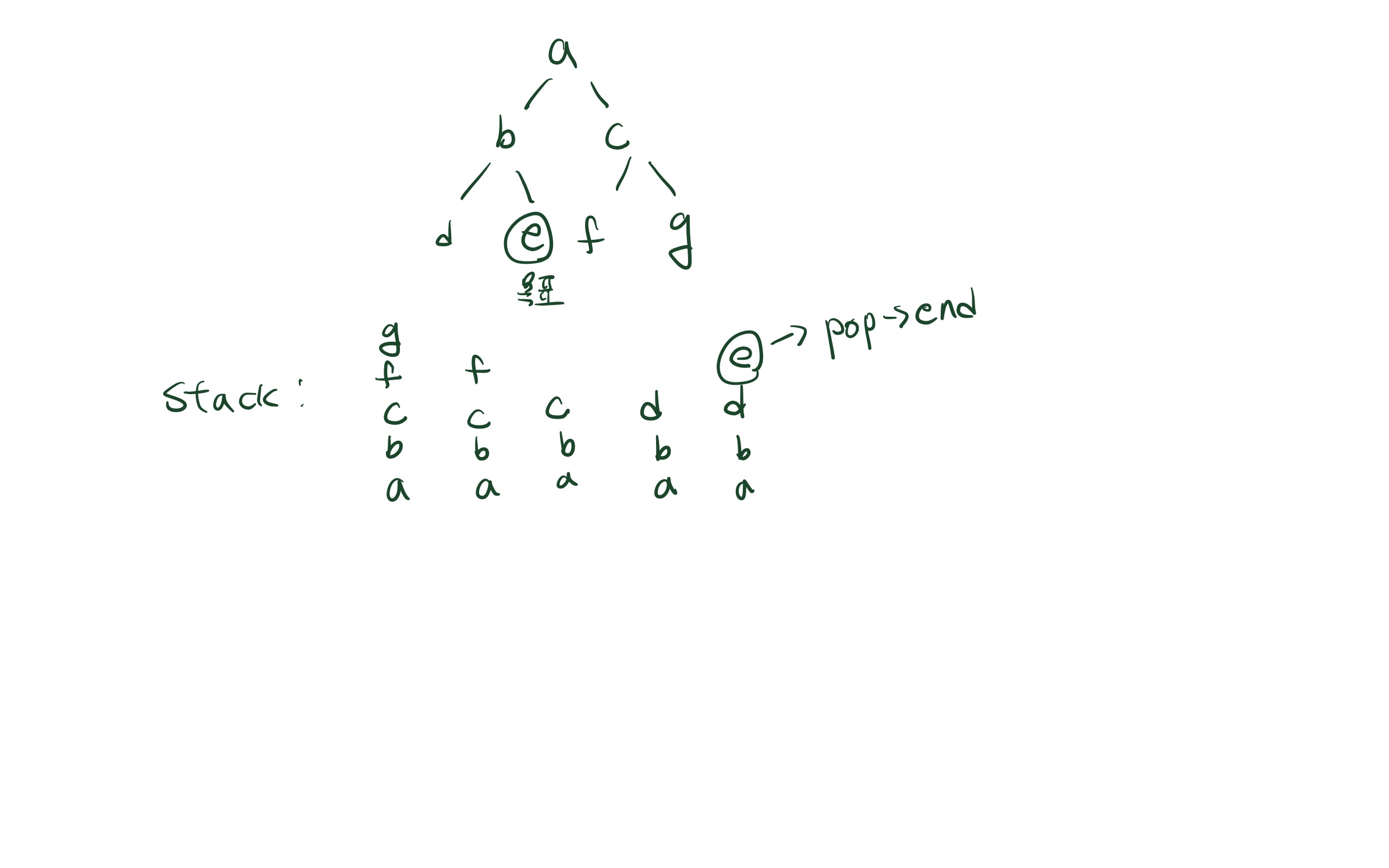
따라서 stack과 visit을 선언하며 시작한다. visit은 방문한 노드를 담아놓음으로써 이미 탐색한 노드를 또 탐색하는 것을 방지한다.
그 후 위, 아래, 왼쪽, 오른쪽으로 움직인, 즉 자식 노드들을 스택에 넣어가며 한 방향으로 탐색한다. 그래프를 모두 탐색했는데도 답이 없을 경우, 즉 움직여서 목표 상태에 도달할 수 없는 경우는 -1을 반환한다.
def movePuzzle(puzzle, x, y, oper):
if(oper == 'up'):
if(x - 1 < 0):
return None
else:
tmp = puzzle[x][y]
puzzle[x][y] = puzzle[x-1][y]
puzzle[x-1][y] = tmp
return puzzle
elif(oper == 'down'):
if (x + 1 >= 3):
return None
else:
tmp = puzzle[x][y]
puzzle[x][y] = puzzle[x + 1][y]
puzzle[x + 1][y] = tmp
return puzzle
elif(oper == 'right'):
if (y + 1 >= 3):
return None
else:
tmp = puzzle[x][y]
puzzle[x][y] = puzzle[x][y + 1]
puzzle[x][y + 1] = tmp
return puzzle
elif(oper == 'left'):
if (y - 1 < 0):
return None
else:
tmp = puzzle[x][y]
puzzle[x][y] = puzzle[x][y - 1]
puzzle[x][y - 1] = tmp
return puzzle
def checkZero(puzzle):
x, y = 0, 0
for i in range(3):
for j in range(3):
if puzzle[i][j] == '0':
x, y = i, j
return x, y0의 위치를 움직이는 코드와 0의 위치를 확인하는 코드이다. 이는 밑의 코드들에 계속 쓰일 함수들이다.
def dfs(puzzle):
goal = [['1', '2', '3'], ['8', '0', '4'], ['7', '6', '5']]
visit = []
stack = [puzzle,]
oper = ['up', 'down', 'right', 'left']
while stack is not None:
current = stack.pop()
if current == goal:
visit.append(current)
return visit
else:
visit.append(current)
x, y = checkZero(current)
for op in oper:
next = movePuzzle(copy.deepcopy(current), x, y, op)
if next is not None and next not in visit:
stack.append(next)
if stack is None:
return -12. BFS (Breadth-First Search) - Queue를 이용하여
BFS는 초기 노드에서 시작하여 모든 자식 노드를 확장하여 생성하고, 모든 자식 노드들을 탐색한다. 만약 목표 노드가 없으면 단말 노드에서 다시 자식 노드를 확장한다. 말 그대로 너비를 기준으로 하는 탐색이다.
초기 노드의 모든 자식을 탐색하고 다시 단말 노드의 자식들을 모두 탐색하는 방식이므로, queue를 이용하여 구현할 수 있다. 한 노드의 자식들이 모두 queue에 담기면 앞에서부터 그 자식들을 모두 탐색해야 하기에 앞에서부터 빠지는 queue가 적합하다. 자세한 설명은 그림으로 대체한다.
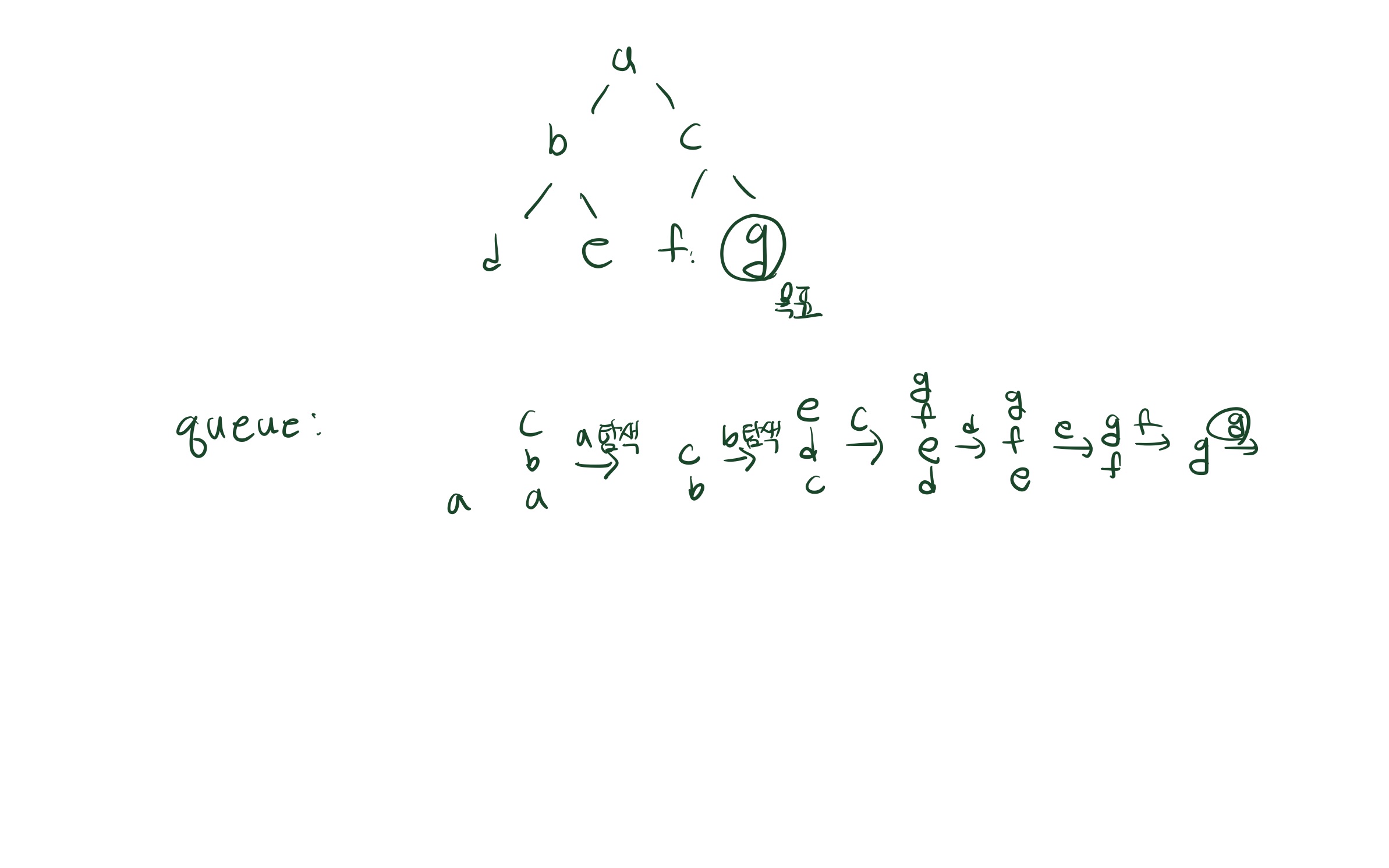
따라서 queue와 visit을 선언하며 시작한다. visit의 역할은 위와 같다. 그림과 같이 한 노드를 방문할 때마다 자식 노드들을 모두 queue에 추가하여 그림과 같은 탐색이 이루어질 수 있도록 한다. 마찬가지로 답을 찾을 수 없는 경우는 -1을 반환한다.
def bfs(puzzle):
visit = []
queue = [puzzle]
goal = [['1', '2', '3'], ['8', '0', '4'], ['7', '6', '5']]
oper = ['up', 'down', 'right', 'left']
while queue is not None:
current = queue.pop(0)
if current == goal:
visit.append(current)
return visit
else:
visit.append(current)
x, y = checkZero(current)
for op in oper:
next = movePuzzle(copy.deepcopy(current), x, y, op)
if next is not None and next not in visit:
queue.append(next)
3. A* 알고리즘
A* 알고리즘은 정보 이용 탐색으로, 추정한 전체 비용을 최소로 하는 노드를 확장해 가는 방법이다. 이는 현재까지 움직인 횟수 (투입된 비용) + 목표 상태와 다른 위치의 갯수 (남은 비용의 추정값) 로 추정한다. 목표 상태와 다른 위치의 갯수 대신 유클리드 거리로 추정하는 방법도 있는데, 이는 추후 구현할 예정이다.
현재까지 움직인 횟수를 구하기 위해 노드를 클래스로 선언한 후 level을 인자로 추가했다. level은 트리에서의 level로, 현재까지 움직인 횟수를 의미한다. f는 추정한 전체 비용, 즉 투입된 비용 + 남은 비용의 추정값 (여기서는 현재까지 움직인 횟수 + 목표 위치와 다른 위치의 갯수), h는 목표 위치와 다른 위치의 갯수이다. 추정한 전체 비용 중 최소를 차례대로 방문하는 방식이므로, queue가 적합하다고 판단되었다. 추정 비용 중 작은 자식들을 모두 탐색하므로 BFS와 비슷하기 때문이다. 단, BFS와 다르게 추정한 전체 비용이 작은 순서대로 방문해야 하므로 자식 노드들을 모두 넣은 후 f값 기준으로 정렬한다. -1이 들어가는 맥락은 BFS, DFS와 같다.
class Node:
def __init__(self, data, hval, level):
self.data = data
self.hval = hval
self.level = level
class Puzzle:
def __init__(self, start):
self.start = start
def h(self, puzzle, goal):
cnt = 0
for i in range(3):
for j in range(3):
if puzzle[i][j] != goal[i][j]:
cnt += 1
return cnt
def f(self, puzzle, goal):
return puzzle.level + self.h(puzzle.data, goal)
def astar(self, puzzle):
visit = []
queue = []
goal = [['1', '2', '3'], ['8', '0', '4'], ['7', '6', '5']]
oper = ['up', 'down', 'right', 'left']
start = Node(data=puzzle, hval=self.h(puzzle=puzzle, goal=goal), level=0)
queue.append(start)
while queue is not None:
current = queue.pop(0)
if(self.h(current.data, goal)==0):
return visit
else:
visit.append(current.data)
x, y = checkZero(current.data)
for op in oper:
next = movePuzzle(copy.deepcopy(current.data), x, y, op)
if next not in visit and next is not None:
queue.append(Node(next, self.h(next, goal), current.level + 1))
queue.sort(key=lambda x:self.f(x,goal), reverse=False)
return -1
'Algorithm' 카테고리의 다른 글
| [Algorithm] 증가하는 부분 수열 leetcode Increasing Triplet Subsequence (0) | 2020.12.20 |
|---|
